Noch haben wir kein Zahlensystem definiert, aber wir wissen, dass es nicht mehr lange dauern kann; auch wissen wir noch aus der Schulzeit, dass wir vorhaben, mit Mengen von Zahlen zu arbeiten.
Wenn man in der Mathematik einen Begriff verwendet, der noch nicht definiert wurde, sagt man, dass man den Begriff naiv benutzt. Noch verwenden wir die verschiedenen Zahlenbegriffe naiv. Beim Begriff
der Menge belassen wir es bei der naiven Verwendung, denn die Theorie der Mengenlehre ist für sich schon eine axiomatisch-deduktive Theorie
(Halmos [26, 26a], Ebbinghaus [13]), der man sich, bei Interesse, zuwenden kann, wenn man die Treppe der Grundlagen
erklommen hat und sich in der großen Empfangshalle des mathematischen Gebäudes umsehen kann.
Unter einer Menge M verstehen wir ein Objekt, das eine Kollektion von wohlunterschiedenen
Objekten ist, welche keiner Anordnung unterliegen müssen und die wir die Elemente von M nennen.
Mit { } symbolisieren wir ein Behältnis, das wir die leere Menge nennen, eine Menge also, die kein Element enthält. Für die nicht-leeren Mengen M: = {a, b, a} und {b, a} =: N, ist M = N ein wahre Aussage,
weil jedes Element nur einmal zählt und die Reihenfolge nicht relevant ist. Wir haben a ∈ N (a ist ein Element von N) und c ∉ M (c ist kein Element von M).
Man verwendet Grafiken nicht, um etwas zu definieren oder zu beweisen, sondern nur, um sich etwas zu veranschaulichen. Zur Veranschaulichung von Mengen eignen sich Venn Diagramme wie in den Abbildungen 1 bis 6.
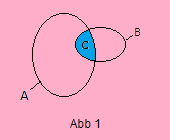
Mit C := A ∩ B = {x | x ∈ A ∧ x ∈ B} ordnen wir C den Durchschnitt oder die Schnittmenge der
Mengen A und B zu (Abb 1).
Ist C nicht leer, sind darin alle Elemente enthalten, die sowohl in A als auch in B enthalten sind).
Ist C leer, sagt man A und B sind disjunkt (Abb. 3).
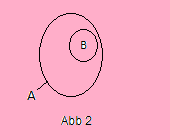
Gilt aber A ∩ B = B, dann schreibt man B ⊂ A (Inklusion) und sagt, B ist eine Teilmenge von A (Abb. 2).
Gilt sowohl B ⊂ A als auch A ⊂ B, dann gilt A = B.
Da { } kein Element enthält, das nicht in jeder anderen Menge enthalten wäre, ist es trivialerweis wahr, dass { } ⊂ M, für jede Menge M.
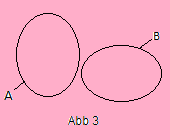
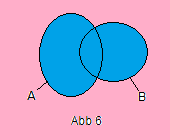
Die Vereinigung zweier Mengen, A ∪ B = {x | x ∈ A ∨ x ∈ B} enthält alle Elemente, aus A und alle Elemente aus B (Abb. 6). Achtung: A ∪ A = A und nicht 2A.
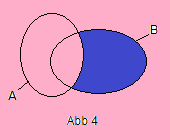
Die Menge die man erhält, wenn man die Elemente von B hernimmt und alle die Elemente entfernt, die auch in A enthalten sind, bezeichnet man als die Differenz B∖A oder B-A (Abb. 4).
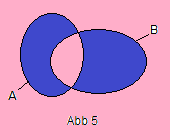
Als die symmetrische Differenz A Δ B zweier Mengen A und B (Abb. 5) bezeichnet man den Ausdruck (A ∖ B) ∪ (B ∖ A) = (A ∪ B) ∖ (A ∩ B).
Einige Bezeichnungen sind für spezielle Mengen reserviert:
∅ := { } (die leere Menge)
N := Menge der natürlichen Zahlen = {1, 2, 3, ...}
N0 := {0, 1, 2, 3, ⋅⋅⋅}
Z := -N ∪ 0 ∪ N = {⋅⋅⋅, -3, -2, -1, 0, 1, 2, 3, ⋅⋅⋅} (die Menge der ganzen Zahlen)
Q := {p∕q | p, q ϵ Z ∧ q ≠ 0}, rationale Zahlen = alle (echten, endlichen und alle periodischen unendlichen) Brüche
R := Menge der reellen Zahlen
C := Menge der komplexen Zahlen, wobei C = {(a + ib) | a,b ∈ R, i2 = -1}
Es gilt: ∅ ⊂ N ⊂ N0 ⊂ Z ⊂ Q ⊂ R ⊂ C
Mit |M| bezeichnet man die Kardinalität oder Mächtigkeit der Menge M. Bei einer endlichen Menge ist die Kardinalität gleich der Anzahl der Elemente in M (also ein n ∈ N ).
Bei einer transfiniten Menge bezeichnet man als Kardinalität die Klasse der Unendlichkeit der Menge M (also ein ℵn ∈ {ℵ0,
ℵ1, ℵ2 ... }). Die abzählbaren unendlichen Mengen
N, Z oder Q, haben die Kardinalität ℵ0 (Aleph-null). Das Kontinuum c, (R), hat die
Kardinalität ℵ1. (Cantorsche Kontinuumshypothese: CH ("Continuum Hypothesis") : 2ℵ0 = ℵ1).
Normalerweise schreiben wir für jede transfinite Menge M, |M| = ∞.
Habe ich eine Menge M mit A ⊂ M, dann heißt B := M∖A das Komplement von A (in M). Beispielsweise bildet die Menge der
geraden Zahlen das Komplement der Menge der ungeraden Zahlen (in der Menge der ganzen Zahlen Z).
Potenzmenge einer Menge
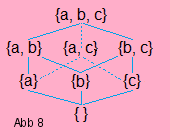
Wir können auch Mengen bilden, deren Elemente Mengen sind. Man hüte sich aber davor, Mengen zu bilden, die sich selbst enthalten. Das ist Unsinn und führt zu Antinomien, wahren Aussagen, deren Negation auch wahr erscheint. Die Potenzmenge P(M) einer Menge M ist die Menge aller Teilmengen von M, inklusive ∅ und M. Ist M := {a, b, c} so ist P(M) := {∅, {a}, {b}, {c}, {a, b}, {a, c}, {b, c}, M}. Bei einer endlichen Menge ist|P(M)| = 2|M|.
Kartesisches Produkt (Mengenprodukt)
Sind A1, A2, ... , An Mengen, so bezeichnen wir mit A1 x A2 x ... x An deren kartesisches Produkt.
Die Elemente dieser neuen Menge werden n-Tupel genannt und haben die Form (a1, a2, ... , an), wobei ai ∈ Ai. Hat
A1 n1 Elemente, gibt es n1 Möglichkeiten die erste Stelle im n-Tupel zu belegen. Für die zweite Position gibt es n2 Möglichkeiten ... , für die letzte Position
gibt es nn Möglichkeiten.
Es ist leicht einzusehen, dass |A1 x A2 x ... x An| = |A1| ⋅ |
A2| ⋅ ... ⋅ |An| ist. Ein Beispiel
für Ai = Aj ist R2 := R x R =: C. Die Elemente von C sind die komplexen Zahlen (a, b).
An erster Stelle in dem 2-Tupel steht der Realteil, an der zweiten Stelle steht der imaginäre Teil. Die Zahl (a, b) wird auch als a + ib bezeichnet.
R x R ist ein gutes Beispiel dafür, dass eine Menge erst ausgestattet mit Axiomen und Operationen einen bestimmten "Verwendungszweck" erhält. Als C stellt R2 die
komplexen Zahlen in der Gaussschen Zahlenebene dar, in der analytischen Geometrie der Ebene ist sie die Menge der Koordinaten der Punkte und in einem 2-dimensionalem Vektorraum kann sie als
Elementmenge fungieren.