So far we have not yet defined any number system, but we know that it won't be long; also we know from school, that we are going to handle sets of numbers.
In mathematics, if we make use of a concept that hasn't been defined yet, we say that we use the concept naively. We still use the different number concepts naively. As far as the concept of a set
is concerned, we leave it at the naive use, because the theory of sets is an axiomatic deductive theory in itself
(Halmos [26, 26a], Ebbinghaus [13]), to which you can devote yourself fully, if you are interested, when you have climbed the
astonishing stairs of the basics and can have a look around in the big reception hall of the mathematical building.
By a set S we mean an object that is a collection of well-distinguished objects, which need not be arranged and which are called the elements of S.
With { } we symbolize a container which we call the empty set, a set, which doesn't contain any element. For the non-empty sets M := {a, b, a,} and {b, a} =: N,
M = N is a true proposition, because every element counts only once, and the order is not relevant. We have a ∈ N (a is an element of N) and c ∉ M (c is not an element of M).
We use Venn diagrams in order to visualize operations with sets, as shown in Abb 1 to 6. (We don't use diagrams to define or prove anything).
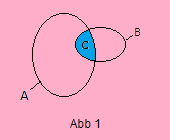
With C := A ∩ B = {x | x ∈ A ∧ x ∈ B} we assign C the intersection of the sets A and B (Abb 1).
If, as result of this operation, C is not empty, it contains all those elements that A and B have in common (Abb 1).
If C is empty, we say that A and B are disjoint (Abb 3).
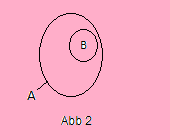
If however A ∩ B = B holds, we write B ⊂ A (inclusion) and call B a subset of A (Abb 2) or we say B is contained in A.
If both B ⊂ A and A ⊂ B hold, then A = B holds.
Since { } contains no element which is not contained in every other set, it is vacuously true that { } ⊂ M for every set M.
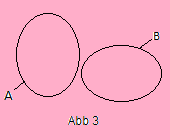
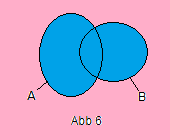
In order to obtain the union of two sets A and B, we empty them into one bag, discard with duplicates and write A ∪ B (Abb 6).
Therefore A ∪ A = {x | x ∈ A ∨ x ∈ A} = A (not 2A).
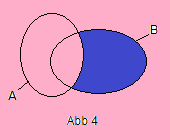
If a set B doesn't want to have something in common with a set A, it removes its intersection with A and calls himself from now on B - A, the
relative complement of A (Abb 4).
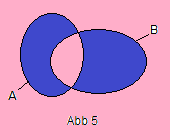
The set A ⊕ B := (A - B) ∪ (B - A) = (A ∪ B) - (A ∩ B)
is called the disjoint union of A and B; see (Abb 5).
The following notations are reserved for standard sets:
∅ := { } (the empty set)
N := the set of natural numbers = {1, 2, 3, ...}
N0 := {0, 1, 2, 3, ⋅⋅⋅}
Z := -N ∪ 0 ∪ N = {⋅⋅⋅, -3, -2, -1, 0, 1, 2, 3, ⋅⋅⋅} (the set of integers)
Q := {p∕q | p, q ϵ Z ∧ q ≠ 0}, the set of rational numbers = all (proper, terminated and all periodic infinite) fractions
R := the set of real numbers
C := the set of complex numbers, where C = {(a + ib) | a,b ∈ R, i2= -1}
We have: ∅ ⊂ N ⊂ N0 ⊂ Z ⊂ Q ⊂ R ⊂ C
With |M| we denote the cardinality of the set M. For a set M having a finite number n of elements, we write |M| = n, for a set M having an infinite number of elements,
we write |M| = ∞. (Cantorsche Kontinuumshypothese: CH ("Continuum Hypothesis") : 2ℵ0 = ℵ1).
If for sets M and A, A ⊂ M holds, we call B := M - A the complement of A (in M). For example, the even numbers form the complement of the uneven numbers
(in the set of the integers Z).
The power set of a set
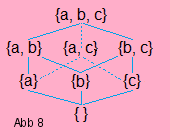
We can also form sets whose elements are sets. But be careful to avoid sets that contain themselves, or similar nonsense. The power set P(M) of a set M is the set of all subsets of M, including ∅ and M. If M := {a, b, c}, then P(M) = {∅, {a}, {b}, {c}, {a, b}, {a, c}, {b, c}, M}. For a finite set M,
|P(M)| = 2|M|.
Set products (Cartesian products)
Let A1, A2, ... ,An be sets. The product of these sets is written A1 x A2 x ... x An. This is a new set, also called the Cartesian product of the Ai and the elements of this new set are called n-tupels which are of the form (a1, a2, ... ,an), where ai ∈ Ai. If A1
has n1 elements, there are n1 possibilities to occupy the first place in the n-tupel. For the second position there are n2 possibilities ... , for the last position there are nn
possibilities. It is now easy to see, that |A1 x A2 x ... x An| = |A1| ⋅ |
A2| ⋅ ... ⋅ |An|.
An example for Ai = Aj ist R2 := R x R =: C. The elements of C are the complex numbers (a, b). The first position in this 2-tupel is occupied by the real part, the second position by the imaginary part.
The number (a, b) is also written as a + ib.
R x R is a fine example of the fact, that a set becomes only "useful", when we provide it with operations and axioms. In the shape of C, R2 constitutes the complex numbers in
the Gaussian number plane, in analytical geometry of the plane it is the set of coordinates of the points of the plane and in a 2-dimensional vector space it serves as set of elements of the space.